非平衡系の物理学
生命現象の情報理論
当研究室では生命現象に代表されるような平衡から遠く離れた系を取り扱うために, 非平衡統計力学と情報理論の境界領域で理論物理の研究をしています. 中でも, 確率過程における熱力学と(古典)情報理論/情報幾何との接点や, 生体システムの情報処理に興味をもって研究を行っています. また機械学習に代表されるような人工的な情報処理や, 確率過程で記述されないようなマクロな系(化学反応, 反応拡散, population dynamics, 流体系)の熱力学における情報論的な側面, 非平衡熱力学・統計力学の理論そのものの発展にも興味を持って研究しています.
非平衡系の物理学から生命現象における情報処理を理解する
学部で習う熱力学・統計力学では, マクロな系の平衡状態および平衡状態間の遷移を取り扱います. ところが我々の周りを見渡していると, 平衡から離れた状態やダイナミックな変化が随所にみられることがわかるでしょう. 特に生命現象においてその傾向は顕著であり, 対象が生きている限り真の意味での平衡状態は達成されていません. このようなダイナミックな現象は一般に非平衡現象と呼ばれ, 熱力学・統計力学のテーマとしても生物物理のテーマとしても重要視されてきました. これまでにも非平衡現象について数多くの重要な発見・発展がなされてきた一方で, 解くべき未解決問題や未解明現象も依然として多く残されています.
中でも, 非平衡現象における興味深いテーマの一つに情報処理が挙げられます. 情報処理は生命現象においても根源的なテーマであり, 生体内では単一分子から細胞集団までの様々なスケールの情報処理によって生体システムが維持されています. しかしながら非平衡現象における情報処理の物理的な理解はまだ限定的で, 特に生命現象に関する理解は根本的に不十分だと考えています. よって, 非平衡現象での情報処理に関する一般的な理論の枠組みを構築することが, 生命現象の理解において重要なステップであると考えて研究しています. またこの枠組みの構築は物理学全体への根本的な貢献にもなるとも考えています.
強い非平衡系の物理理論を開拓する
強い非平衡系においてはダイナミックな振る舞いや, ポテンシャルで記述できないような非保存的な駆動が存在することで, 通常の平衡統計力学・平衡熱力学や平衡近傍系における非平衡熱力学の記述・手法が使えないことがあります. 我々は系を限定せず, 量子系・古典確率過程・化学反応系・流体系・反応拡散系・ポピュレーションダイナミクスや小自由度系・大自由度系, 対称性の高い系や低い系など, さまざまな非平衡系において成り立つような普遍的な手法の開発や法則性の探求を行なっています. 特に我々は近年発展が著しいゆらぎの熱力学などの非平衡物理学・統計力学の理論や情報理論/情報幾何・最適輸送理論・グラフ理論・線形代数などの数学に立脚して, 新たな物理法則と解析手法を開拓しています.
これまでの研究
ネットワーク上の情報熱力学
近年, 非平衡現象の研究の中でも, マクロとミクロの間の中間領域であるメゾスコピックなスケールを記述可能な確率過程における熱力学の理論(ゆらぎの熱力学)が発展しています. このゆらぎの熱力学は, 分子モーターや生化学ネットワークなどの生体システムへの適用が可能であり, 生命現象の基礎的な物理理論の一つとして着目されています. その中でも我々は熱力学と情報理論の接点「情報熱力学」に興味を持って研究をしており, 生体システムにおける情報処理の熱力学的な制約を, 系の詳細に依らない普遍的な法則性を通じて理解しようとしています.
特にMaxwellのデーモンの議論に端を発する熱力学的なエントロピーと情報量の間の関係は, 情報項を含んだ形での熱力学第二法則の一般化として定式化されることで理解が進んでいます. 我々はベイジアンネットワークと呼ばれる確率的な相関を記述する手法やマルコフネットワークの理論(Schnakenberg)などを用いて, 複雑に相互作用する自律的な系において熱力学第二法則を一般化し, 情報の流れの各指標(相互情報量, transfer entropy, learning rate, directed informationなど)が, どのように熱力学第二法則やオンサーガ相反関係の一般化に影響を与えるかを調べてきました.
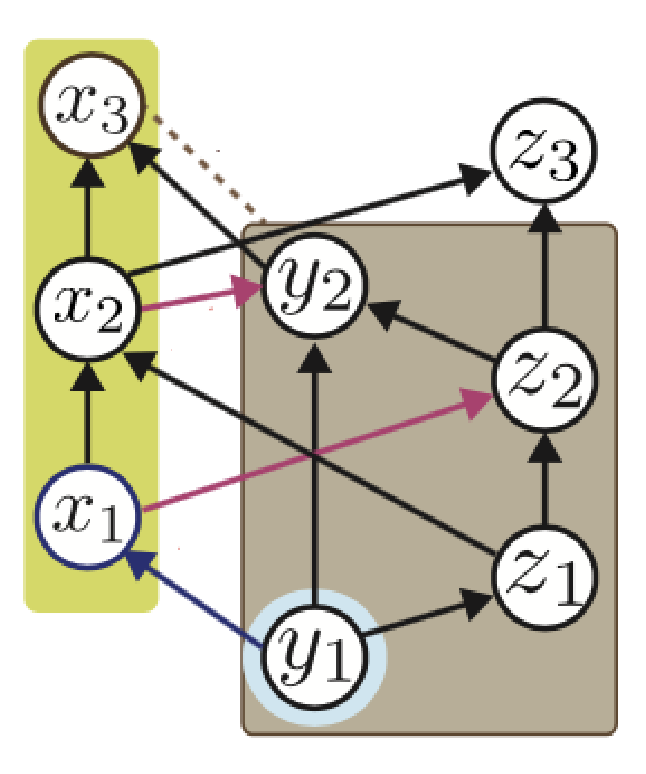
E.coli走化性シグナル伝達の情報伝達と情報熱力学
我々はさらにネットワーク上の情報熱力学をもちいて, E.coli(大腸菌の一種)の走化性シグナル伝達での受容体のメチル化による適応のダイナミクスを, 情報処理の熱力学的な性能の観点から考察しました. 特に, 情報項を含んだ形での熱力学第二法則を利用することで, 入力のノイズに対する出力の頑健性(ロバストネス)が, シグナルネットワーク中に流れる情報によって抑えられるという法則性を調べ, 通信路符号化定理に代表されるような情報理論との関係を調べました.
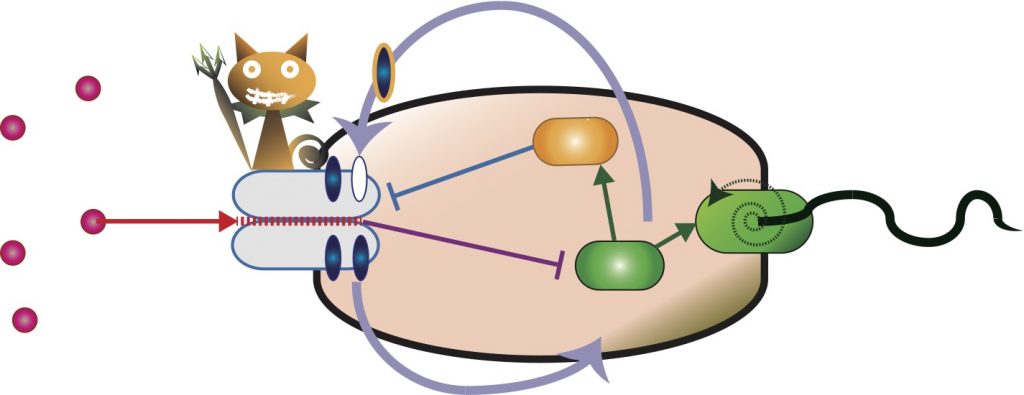
大腸菌に潜む「マクスウェルのデーモン」の働きを解明―情報と熱力学の融合による生体情報処理の解析への第一歩―
ゲーム理論的な情報熱力学
情報熱力学を部分系の熱力学だとみなした場合, 複数の部分同士の散逸を個別に考えることができます. 生体センサーなどの系においては, 部分系同士が共同して機能を実現しており, 情報熱力学の議論が用いられています. そこで我々は, それぞれの部分の散逸を最小化しながらも, 部分系同士が共同して平衡近傍である遷移を行うという熱力学的にコンフリクトのある状況を, 最適輸送問題の亜種としてゲーム理論的に考察しました. ナッシュ均衡解として得られた結果によると, それぞれの部分同士の最小散逸は達成したい遷移の重要度によってトレードオフが発生することがわかりました. また大腸菌の走化性における適応センサーにおいて各部分系で散逸に大きな差が生まれている現状を, 部分系の最小散逸と機能の達成における遷移の重要度という観点から進化論的に説明しうることを議論しました.
情報幾何とゆらぎの熱力学, 情報熱力学
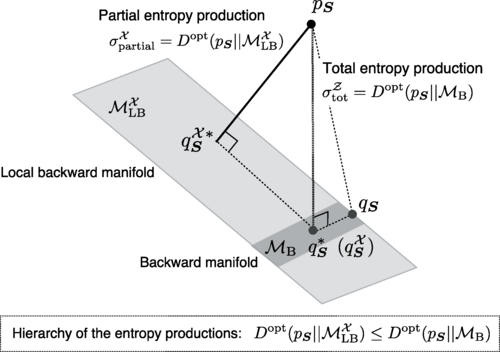
また我々は情報幾何を用いたゆらぎの熱力学及び情報熱力学の整理や, 理論の拡張にも興味を持っています. そこで, まずは熱力学第二法則と情報熱力学第二法則の結果を, 情報幾何における射影の観点から整理できることを明らかにし, 部分と全体の間の関係から統合情報理論の一種であるstochastic interactionとの関係を議論しました. また緩和するダイナミクスにおける、ゆらぎの熱力学における熱力学力と流れと情報幾何学的な双対な座標の関係について議論しました. 情報幾何の双対構造を使うことで、非平衡自由エネルギー(エントロピー生成)と、外場下の平衡自由エネルギーとが、Legendre 変換で結びつくことを発見しました. この関係を応用して、外場下の平衡状態での測定から、緩和過程のエントロピー生成を推定する手法を構成しました.
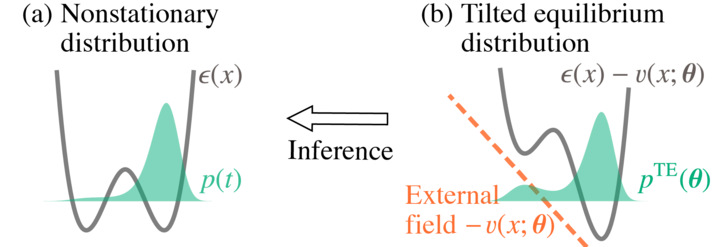
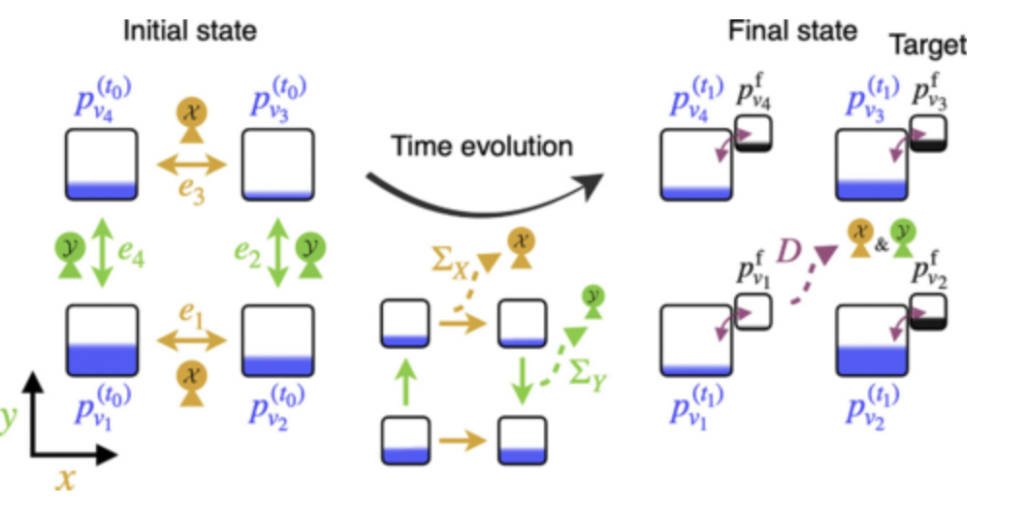
化学熱力学とゆらぎの熱力学のアナロジー
我々は近年, 決定論的な力学系であるレート方程式によってダイナミクスが記述される化学反応ネットワークにおける化学熱力学と, 確率分布の時間発展で表されるマスター方程式上のゆらぎの熱力学の間のアナロジーについて考察しています. 例えば, ゆらぎの熱力学における情報幾何のアナロジーとして, ギブスの自由エネルギーが一般化KLダイバージェンスと呼ばれる情報理論の言葉で記述可能であることを用いて, 熱力学的なトレードオフ関係についての研究を行いました. またゆらぎの熱力学で研究されていた熱力学的不確定性関係と熱力学的速度制限について, 化学熱力学における対応物についての研究を行いました. また、化学熱力学で基本的なギブス自由エネルギーを用いて、情報幾何学的な構造を表す双対座標系を具体的に構成しました. これにより、化学熱力学とゆらぎの熱力学が統一的な情報幾何構造を持つことを明確に示しました.
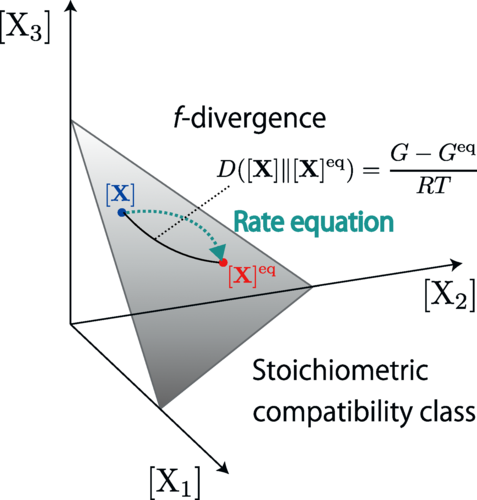
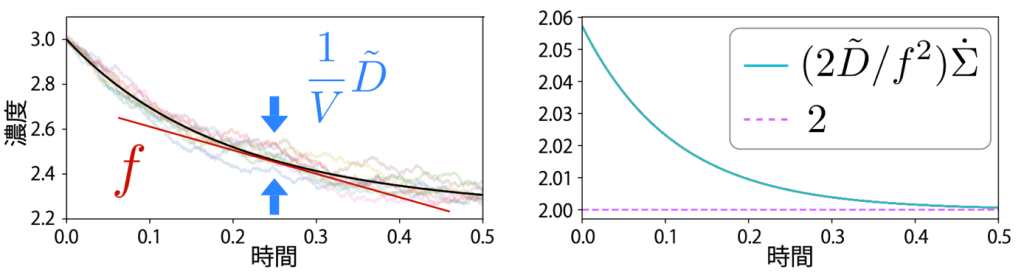
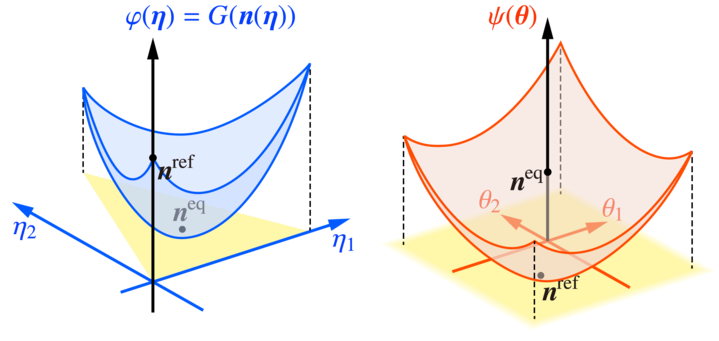
最適輸送理論とゆらぎの熱力学、Wasserstein幾何学
我々はゆらぎの熱力学と情報幾何学の対応関係と同様の手法で, 確率分布における微分幾何学的な理論である最適輸送理論を用いてゆらぎの熱力学を幾何学的に捉え直す研究も行っています. 特にブラウン運動における確率分布の最適な輸送を考えることで, エントロピー生成のWasserstein幾何学的な表現と, その幾何学的な表現を用いた最小エントロピー生成を与える熱力学的速度限界や, エントロピー生成の定常状態熱力学的なexcessとhousekeepingと呼ばれる二つの寄与への幾何学的な分解, 及び射影の観点から定常状態熱力学における熱力学的不確定性関係を導出しました.
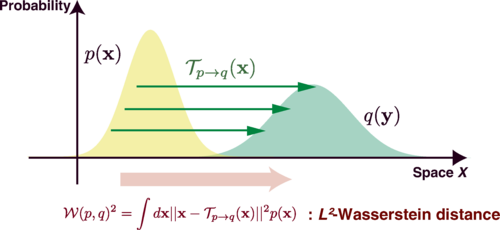
Nakazato, M., & Ito, S. (2021). Geometrical aspects of entropy production in stochastic thermodynamics based on Wasserstein distance. Physical Review Research, 3(4), 043093.
population dynamicsにおける情報幾何的な速度限界
我々はpopulation dynamicsにおけるトレードオフ関係を, 情報幾何を用いて探る研究も行なっています. 特に増殖と変異が独立に起きるモデルに対し, 増殖の効果と変異の効果のそれぞれに対応する部分的なFisher情報量に注目することで, population dynamicsに特有の新しい速度限界を見出しました. またFisherの自然選択の基本定理の位置表現であるPrice方程式の情報幾何学的な解釈と, その拡張についても議論しています.
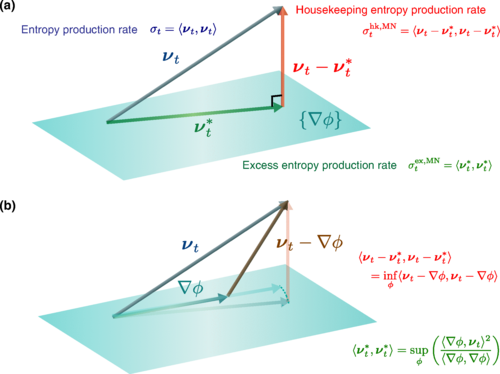
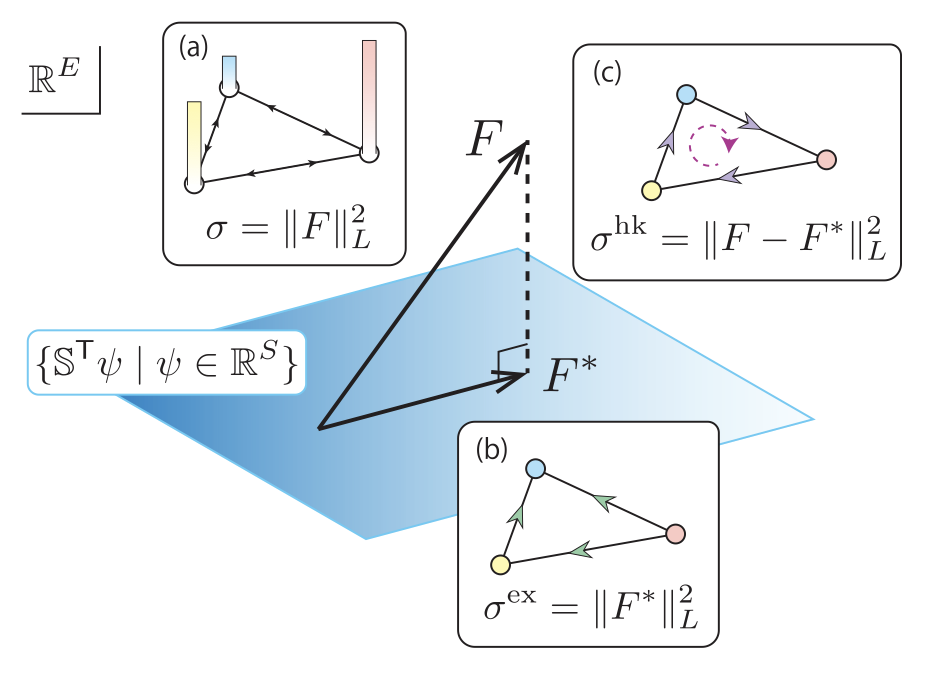
確率過程, 決定論的な化学反応系における熱力学的散逸の幾何学的な分解と熱力学的トレードオフ関係
我々は一般的な非平衡系を表す確率過程であるMarkovジャンプ系や決定論的な力学系であるレート方程式におけるダイナミクスで, 保存力による時間発展と非保存力による状態の維持の二つの寄与を幾何学的に分解する手法を, 最適輸送理論に基づいて導入しました. そして保存力による時間変化に本質的な散逸(excessエントロピー生成率)と非保存力による時間変化によらない散逸(housekeepingエントロピー生成率)の二つの寄与に散逸の分解を行い, それぞれの散逸が状態の時間変化の速さや状態の流れに関する揺らぎなどに対する限界(熱力学的不確定性関係, 熱力学的な速度限界)を与えることを見出しました. また保存力による時間変化に本質的な散逸(excessエントロピー生成率)からWasserstein距離という量で表される幾何的な構造を導入できることも示しました.
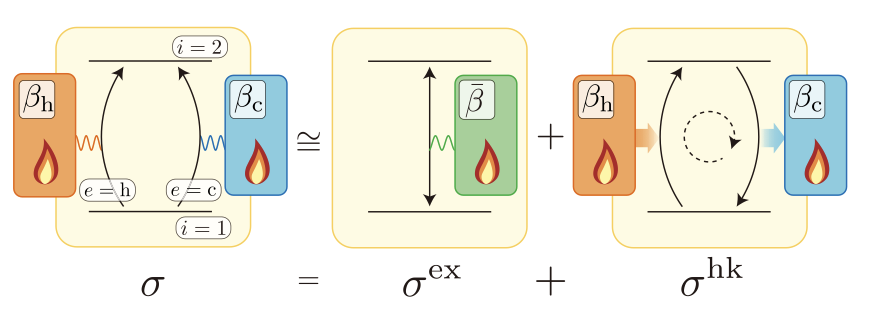
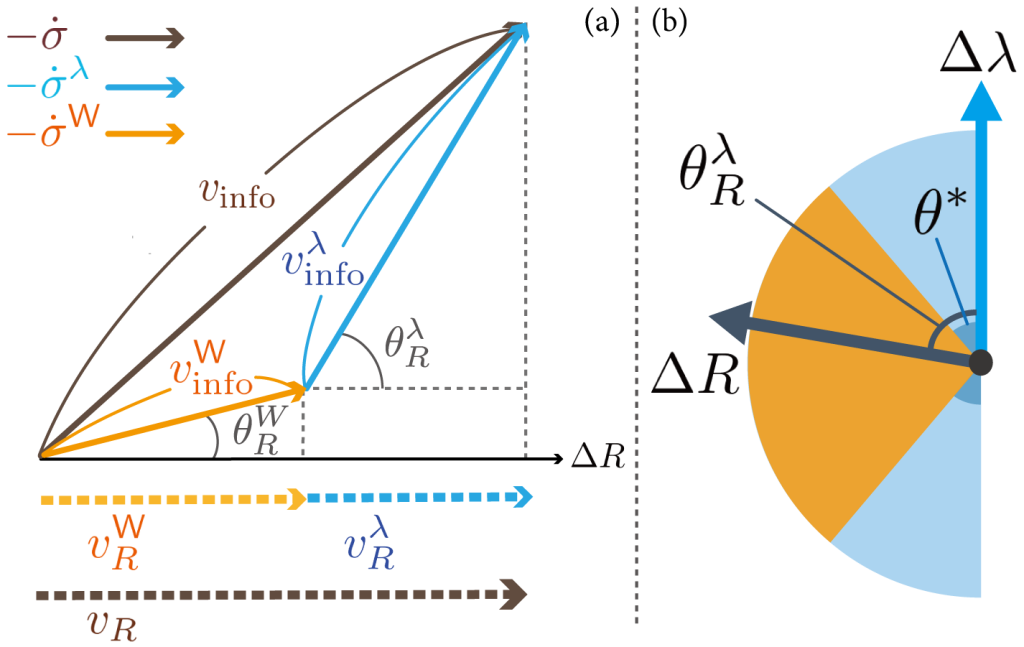
相関関数の非対称性と非平衡性の間の普遍的な関係
平衡状態において相関関数は対称性を持つことが, ミクロなOnsager相反関係の一種(microscopic reversibility)として知られています。このmicroscopic reversibilityは系が平衡状態から外れた場合には成り立たず, 相関関数は一般に対称性を示さないことで非対称な情報の流れが発生することが可能になります. そこで我々は非平衡状態の一つの指標である熱力学的駆動力の大きさが相関関数の非対称性の大きさの限界を与えることを, 等周不等式などの幾何学的な不等式を利用して普遍的に示し, 非平衡系におけるミクロなOnsager相反関係の一種を一般化しました. またこの結果から得られる帰結として, これまで体内時計の数理モデルなどで減衰振動する緩和の振る舞いにおける, コヒーレントな振動の数と熱力学的駆動力の間の不等式が数値的に予想されていたものを, 肯定的に証明することに成功しました.
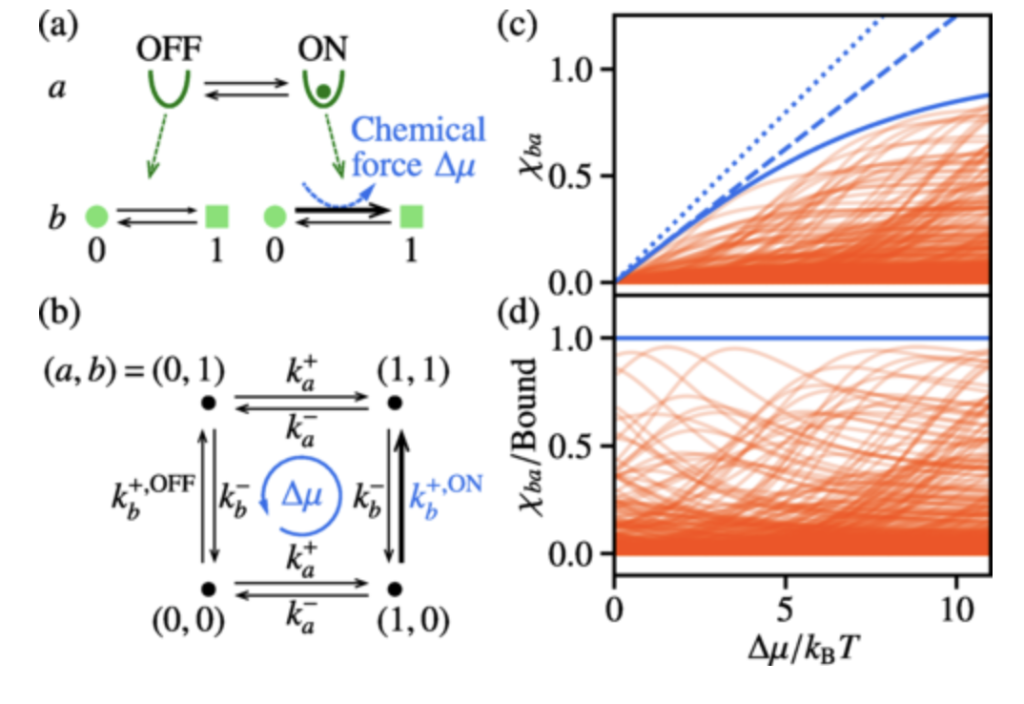
非平衡性による緩和の振る舞いに関する熱力学的な限界
Markovな確率過程で駆動される系においては, 遷移レートの行列の固有値の集合, すなわちスペクトルが緩和の振る舞いを決めます. 平衡状態に緩和する場合は単調な緩和が見られる一方で, 非平衡定常状態に緩和する場合は振動したり緩和の速さが加速することが, スペクトルの性質から理解されてきました. そこで我々は, 平衡状態に緩和する場合と非平衡定常状態に緩和する場合の間のスペクトルの違い(スペクトルギャップ)が, 非平衡定常状態における散逸とどのように関係するかを調べ, 非平衡定常状態における散逸の大きさが大きいほどスペクトルギャップが大きくなり, 緩和の速さの加速や減衰振動が生まれることを普遍的な不等式として示しました.
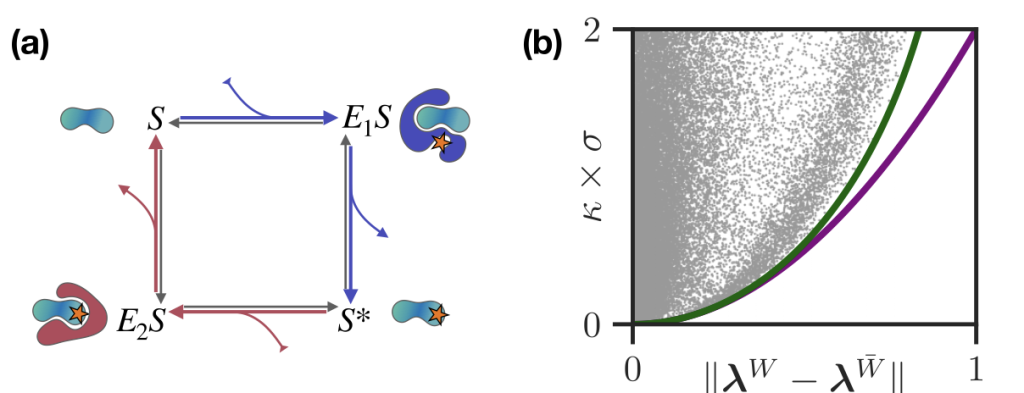
流体系における熱力学とゆらぎの熱力学とのアナロジー
ナビエ=ストークス方程式で記述されるようなマクロな流体系においては古くから熱力学が議論されています. 我々は近年発展してきたブラウン運動系の非平衡熱力学であるゆらぎの熱力学と流体系の熱力学のアナロジーを導入することで, ゆらぎの熱力学の数理的な手法をナビエ=ストークス方程式で記述される圧縮性ニュートン流体に導入しました. そして熱力学的な散逸であるエントロピー生成率の保存力と非保存力による幾何学的な分解や, 散逸と状態のゆらぎと状態変化の速さとの間のトレードオフ関係である熱力学的不確定性関係が, マクロな流体系においても成り立つことを示しました. また本結果の一部は非圧縮性流体において成り立つHelmholtzによる最小散逸定理の一般化にもなっていることを見出しました.
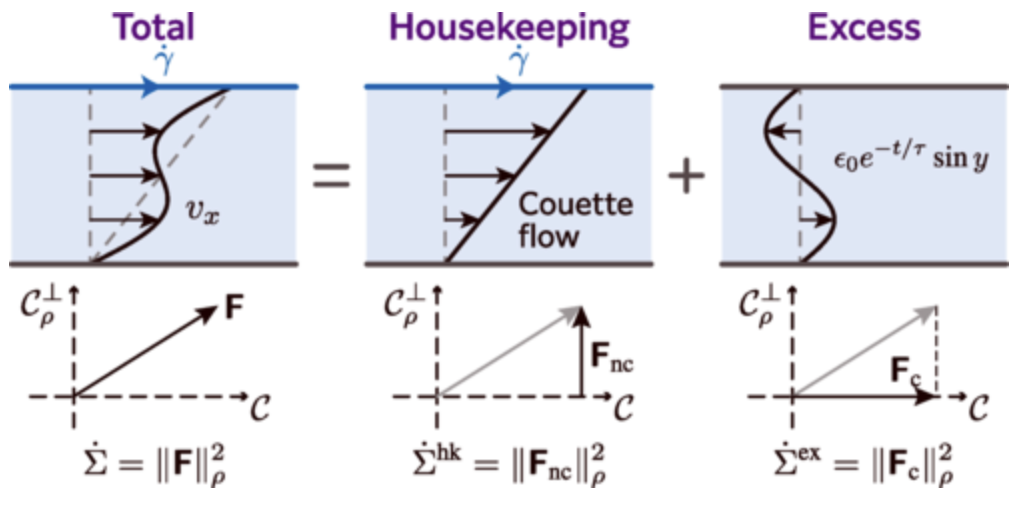
脳ダイナミクスにおける脳波に対する熱力学的な不可逆性の周波数分解
線形なLangevin方程式において統計的な不可逆性の指標であるエントロピー生成率を, 保存力による寄与(excess)と非保存力による寄与(housekeeping)に幾何学的に分解すると, 非保存力による寄与は純粋な振動のモードによる寄与であることがわかりました. そこで我々は動的モード分解と呼ばれる手法のアナロジーを用いて, 非保存力による散逸(housekeepingエントロピー生成率)を振動モードごとに分解する手法を開発しました. またこの開発した手法をサルの皮質脳波データ(ECoG)に適用して, サルの脳の統計的な不可逆性が麻酔下と覚醒時でどのように違いうるかを, 各脳波の振動モードごとの寄与の視点から解析しました. それによると, 麻酔下では統計的な不可逆性が覚醒時よりも高く, それはデルタ波などの遅い脳波のモードによって引き起こされていることがわかりました.
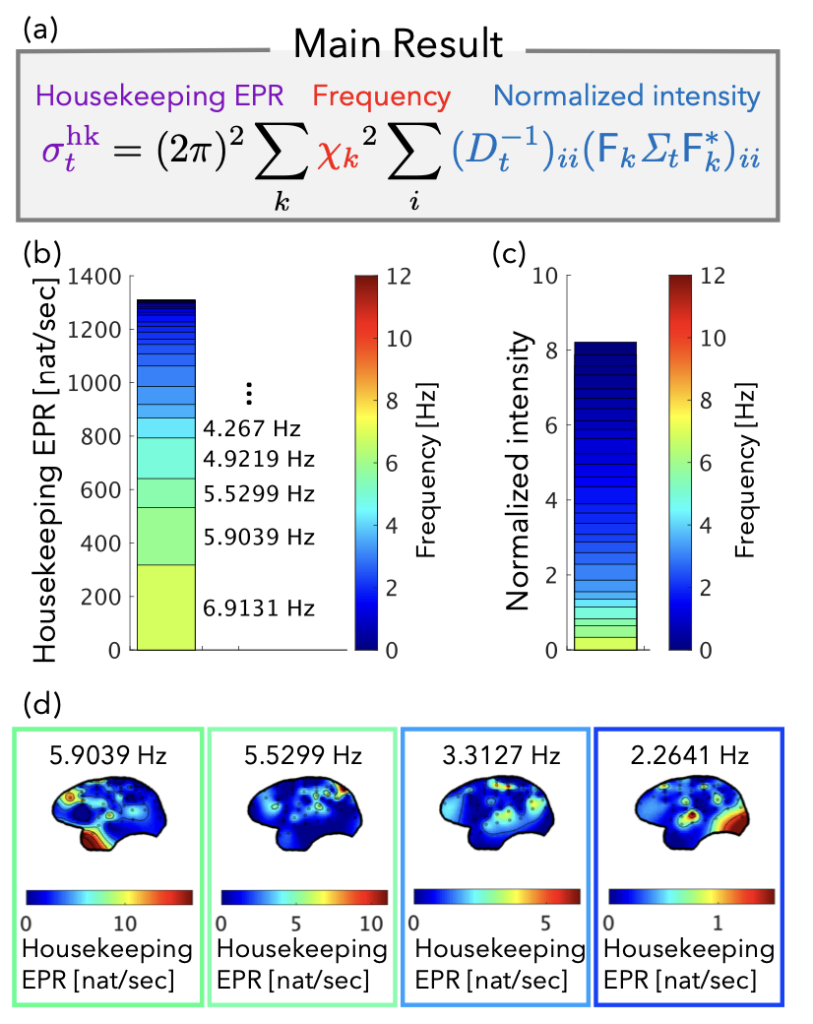
Daiki Sekizawa, Sosuke Ito, and Masafumi Oizumi ”Decomposing Thermodynamic Dissipation of Linear Langevin Systems via Oscillatory Modes and Its Application to Neural Dynamics” Physical Review X 14, 041003 (2024).
パターンダイナミクスにおける最適輸送と、熱力学的な散逸とパターン変化のトレードオフ
我々は最適輸送理論における手法をマクロな反応拡散系において拡張することで, 反応拡散系における熱力学的な散逸とパターンの変化に代表されるような状態の変化の間のトレードオフ関係を導くことに成功しました. また大きな波数によるパターンの荒い変化よりも, 小さな波数によるパターンの詳細な変化の方が熱力学的な散逸を必要とすることを熱力学的な不確定性関係という普遍的な関係式の形で示しました. さらに最適輸送理論を拡張してパターン間の距離(Wasserstein距離)を導入することで, 熱力学的に整合的なパターン間の距離構造を導入しました.
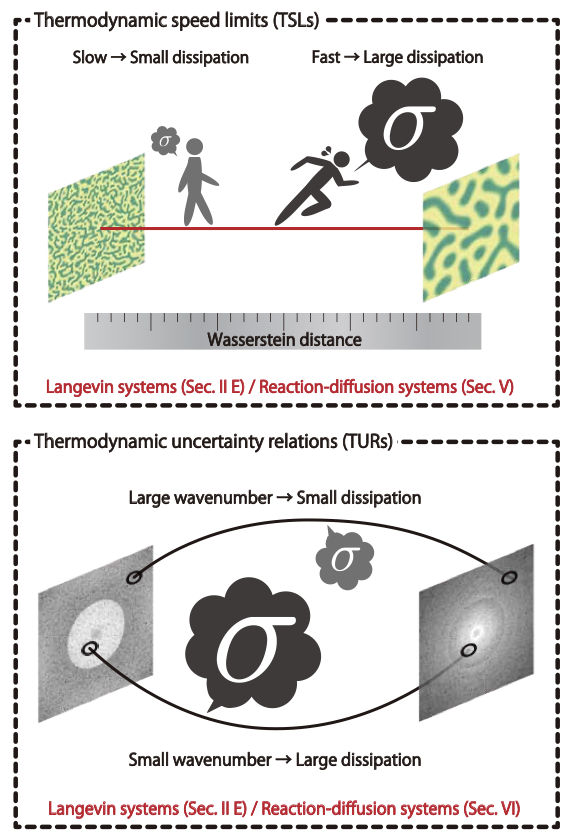
Ryuna Nagayama, Kohei Yoshimura, Artemy Kolchinsky, Sosuke Ito ”Geometric thermodynamics of reaction-diffusion systems: Thermodynamic trade-off relations and optimal transport for pattern formation” Physical Review Research 7, 033011 (2025).
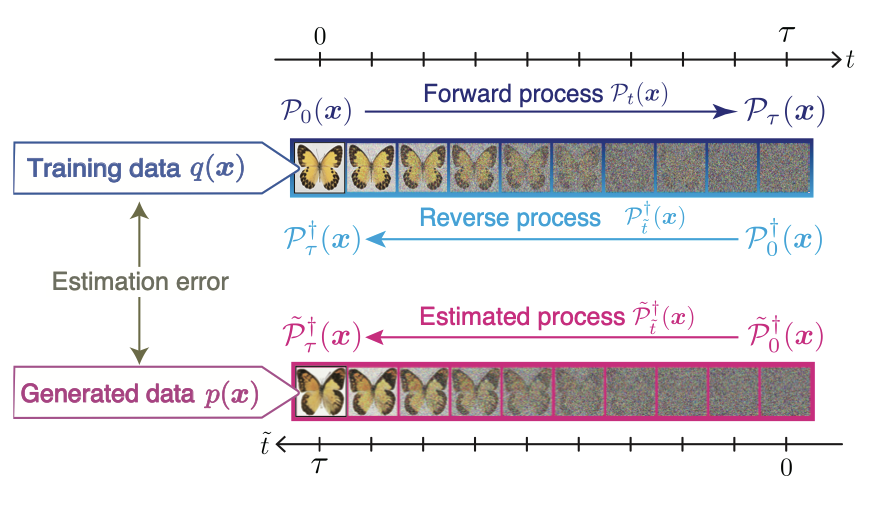
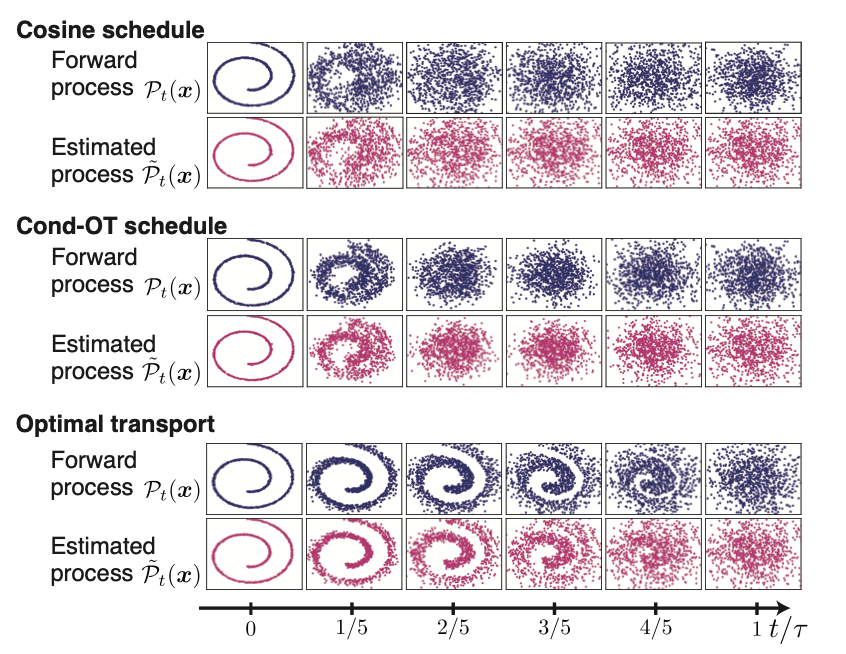
生成AIの手法である拡散モデルにおける生成精度の熱力学的な限界
Stable diffusionなどの画像生成AIに代表される生成AIの数理的な基盤である拡散モデルにおいて, 最適輸送に基づいた手法が生成精度を上げることが経験的にこれまで知られてきました. そこで我々は拡散モデルの数理に非平衡熱力学の知見を導入しました. 最適輸送に基づいた非平衡熱力学の手法を応用することにより, 拡散モデルによって生成されたデータの生成精度と拡散ダイナミクスから導入される熱力学的な散逸であるエントロピー生成率と呼ばれる量の間のトレードオフ関係を見出しました. また得られたトレードオフ関係は拡散が保存力で駆動されるような具体的な状況では最適輸送理論によって解釈することができ, 我々が用いた生成精度の指標が最も高くなりうる状況は最適輸送の状況であることを示すことに成功しました.
情報幾何と最適輸送理論の関係の数理的展開
Fokker-Planck方程式において, 情報幾何において主役となるKullback-Leiblerダイバージェンス, Fisher情報量, 射影定理, クラメル=ラオ不等式などと, 最適輸送理論の幾何において主役となるWasserstein距離やgradient flow, およびgradient flowに関連する不等式についてのアナロジーや関係性について, 熱力学的なエントロピー生成を経由しながら議論し, 確率分布の世界での異なる二つの幾何学の融合に関する開拓を行なっています.